Atualmente, o processo de expansão ocupacional utiliza os mesmos princípios criados nos séculos anteriores. A diferença é que hoje as medidas são padronizadas de acordo com o Sistema Internacional de Medidas. Dentre as medidas de área existentes temos:
km²: quilômetro quadrado
hm²: hectômetro quadrado
dam²: decâmetro quadrado
m²: metro quadrado
dm²: decímetro quadrado
cm²: centímetro quadrado
mm²: milímetro quadrado
Uma área com 1 km² equivale a uma região quadrada com lados medindo 1 km e para as outras medidas segue-se o mesmo raciocínio. De acordo com o Sistema de Medidas, a unidade padrão para a representação de áreas é o m² (metro quadrado). Utiliza–se o km² em situações relacionadas à medição de áreas de cidades, estados, países, continentes, etc.
Na Geometria, as formas mais conhecidas são: triângulo, quadrado, retângulo, paralelogramo, losango, trapézio e círculo. Todas essas formas possuem fórmulas matemáticas para o cálculo da medida de suas superfícies. Para o cálculo de área envolvendo as figuras mais complexas desenvolvemos cálculos matemáticos específicos entre outras técnicas.
Nesta seção iremos abordar o cálculo da superfície das principais formas planas existentes, relacionando a figura com sua fórmula matemática.
hm²: hectômetro quadrado
dam²: decâmetro quadrado
m²: metro quadrado
dm²: decímetro quadrado
cm²: centímetro quadrado
mm²: milímetro quadrado
Uma área com 1 km² equivale a uma região quadrada com lados medindo 1 km e para as outras medidas segue-se o mesmo raciocínio. De acordo com o Sistema de Medidas, a unidade padrão para a representação de áreas é o m² (metro quadrado). Utiliza–se o km² em situações relacionadas à medição de áreas de cidades, estados, países, continentes, etc.
Na Geometria, as formas mais conhecidas são: triângulo, quadrado, retângulo, paralelogramo, losango, trapézio e círculo. Todas essas formas possuem fórmulas matemáticas para o cálculo da medida de suas superfícies. Para o cálculo de área envolvendo as figuras mais complexas desenvolvemos cálculos matemáticos específicos entre outras técnicas.
Nesta seção iremos abordar o cálculo da superfície das principais formas planas existentes, relacionando a figura com sua fórmula matemática.
As figuras são:
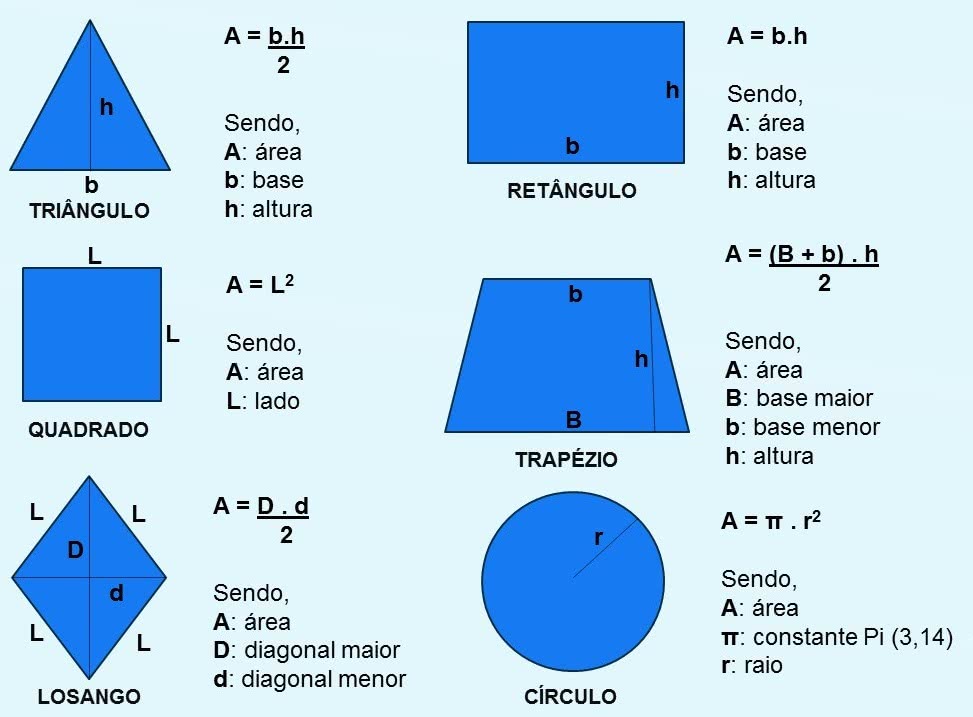
PROPRIEDADES DA GEOMETRIA PLANA:
- Ponto
Conceito adimensional, uma vez que não possui dimensão. Os pontos determinam uma localização e são indicados com letras maiúsculas.
- Reta
A reta, representada por letra minúscula, é uma linha ilimitada unidimensional (possui o comprimento como dimensão) e pode se apresentar em três posições:
- horizontal
- vertical
- inclinada
Dependendo da posição das retas, quando elas se cruzam, ou seja, possuem um ponto em comum, são chamadas de retas concorrentes.
Por outro lado, as que não possuem ponto em comum, são classificadas como retas paralelas.
- Segmento de Reta
Diferente da reta, o segmento de reta é limitado pois corresponde a parte entre dois pontos distintos.
A semirreta é limitada somente num sentido, visto que possui início e não possui fim.
- Plano
Corresponde a uma superfície plana bidimensional, ou seja, possui duas dimensões: comprimento e largura. Nessa superfície que se formam as figuras geométricas.
- Ângulos
São formados pela união de dois segmentos de reta, a partir de um ponto comum, chamado de vértice do ângulo. Os ângulos são classificados em:
- ângulo reto (Â = 90º)
- ângulo agudo (0º < Â < 90º)
- ângulo obtuso (90º < Â < 180º)
- Área
A área de uma figura geométrica expressa o tamanho de uma superfície. Assim, quanto maior a superfície da figura, maior será sua área.
- Perímetro
O perímetro corresponde a soma de todos os lados de uma figura geométrica.
Exercícios:
1º)
(UFMT) Assinale a medida do lado de um quadrado, sabendo-se que o número que representa o seu perímetro é o mesmo que representa sua área.
a) 5
b) 4
c) 6
d) 8
2º)
Uma escola pretende ladrilhar o seu pátio retangular, que possui as seguintes dimensões: 4 m e 5,5 m. Os ladrilhos utilizados são quadrados com 16 cm de lado. Calcule o número de ladrilhos necessários.
3º)
Um campo de futebol de formato retangular tem 100 metros de largura por 70 metros de comprimento. Antes de cada treino, os jogadores de um time dão cinco voltas e meia correndo ao redor do campo. Sendo assim, determine:
a) Quantos metros os jogadores correm ao dar uma volta completa no campo?
b) Quantos metros eles percorrem ao dar as cinco voltas e meia ao redor do campo?
c) Se eles repetem essa corrida cinco vezes por semana, quantos metros os jogadores correm em uma semana?
4º)
Determine a área das seguintes figuras (em cm):
________________________________________________________________
RESPOSTAS::
1º)
Para solucionar essa questão, devemos determinar a medida dos segmentos BP, PA, BM, MC, AN e NC. Essas medidas são estabelecidas por meio do ponto médio, que é o ponto que divide o segmento em duas partes iguais. Observe no desenho as medidas dos segmentos de acordo com os seus três pontos médios: M, N e P.
Agora que sabemos as medidas dos segmentos descritos anteriormente, podemos calcular a área.
Dados para o cálculo da área do triângulo MCN:
a = base
2
b = altura
2
Fórmula para calcular a área do triângulo: A = base . altura
2
Cálculo da área do triângulo MCN:
AMCN = a . b
2 2
2
AMCN = ab . 1
4 2
AMCN = ab
8
8 . AMCN = ab
Dados para o cálculo da área do triângulo BAC:
a = base
b = altura
Fórmula para calcular a área do triângulo: A = base . altura
2
Cálculo da área do triângulo MCN:
ABAC = a . b
2
ABAC = 8 . AMCN
2
ABAC = 4 AMCN
ABAC = 3 AMCN + AMCN
Logo, AABMN = 3 AMCN
A área a ser calçada corresponde a 3 AMCN . Letra “e”.
_______________________________________________________
2º)
Dados da questão:
Dimensão do pátio: 4 m e 5,5 m
Dimensão do lado do ladrilho: 16 cm → 0,16 m
Cálculos:
Área total do pátio = 4 m x 5,5 m = 22 m2
Área do ladrilho = (0,16 m)2 = 0,0256 m2
Quantidade de ladrilhos necessários: 22 m2 : 0,0256 m2 = 859, 375 ladrilhos.
São necessários aproximadamente 859 ladrilhos para cobrir toda a área do pátio da escola.
______________________________________________________________________
3º)
a) Vamos calcular o perímetro do campo:
2p = 100 + 100 + 70 + 70
2p = 200 + 140
2p = 340 m
Ao dar uma volta completa, os jogadores percorrem 340 metros.
b) Se ao dar uma volta, os jogadores percorrem 340 metros, ao dar cinco voltas, eles percorrem 340 * 5 = 1700 metros. Para cinco voltas e meia, ele vai andar os 1700 metros e metade de uma volta (340 : 2 = 170). Basta somar 1700 +170: 1870 metros.
c) Considerando que os jogadores correm 5 vezes por semana, se todos os dias eles correm 1870 metros, façamos 1870 * 5 = 9.350. Em uma semana, os jogadores correm 9.350 metros.
__________________________________________________________
4º)
Resposta a:
Retângulo amarelo:
2*3 = 6
Retângulo verde:
2*6 = 12
Retângulo azul:
10*3 = 30
A soma de todos eles:
6 + 12 + 30 = 48cm²
Resposta b:
Área do triângulo:
(3*3)/2 = 4,5
Retângulo laranja:
4* (3+3) = 24
Retângulo rosa:
2*5 = 10
A soma de todas figuras:
4,5 + 24 + 10 = 38,5cm²
_________________________________________________________________________
______________________________________________________________________



Nenhum comentário:
Postar um comentário